The Magnitude System - How To Understand the Brightness of Stars and Planets
October 31, 2017Discuss this article in the forumsTo describe the brightness of objects in the sky, astronomers use a numerical measure called magnitude. It's a bit of a confusing concept for new stargazers, at least a first. But with a little practice, it's not too hard to follow how the magnitude system works. Once you understand it, you can follow sky tours and star atlases, and you can evaluate the quality of the night sky on a given night. Here's how it all works.
1. An Ancient System
The modern magnitude system that describes the brightness of stars and planetshas its roots in the work of the ancient Greek astronomer Hipparchus in the 2nd century B.C. In this system, brighter stars and planets have a smaller numerical value of magnitude than fainter objects. So, for example, a star of magnitude 4 is brighter than a star of magnitude 5.
It's easier to remember this reversed system when you think of the meaning of the word magnitude, that is, "the greatness of rank or position".So a star of first magnitude must be greater (or brighter) than a star of second magnitude, and a star of the second magnitude must be greater (or brighter) than a star of third magnitude, and so on. That's how the Greeks thought of it, and the system has been with us ever since.
To be more precise, the magnitude system is defined such that an object with magnitude 1.0 is exactly 100 times brighter than an object with magnitude 6.0. So each step of 1.0 in magnitude is the fifth root of 100, which works out to a factor of 2.512. That means a star of magnitude 3.0 is about 2½ times brighter than a star of magnitude 4.0, which is about 2½ times brighter than a star of magnitude 5.0, and so on. Try it yourself, if you have a calculator handy, and do the calculation from magnitude 1.0 to 6.0. It works out to a factor of 2.5125=100.
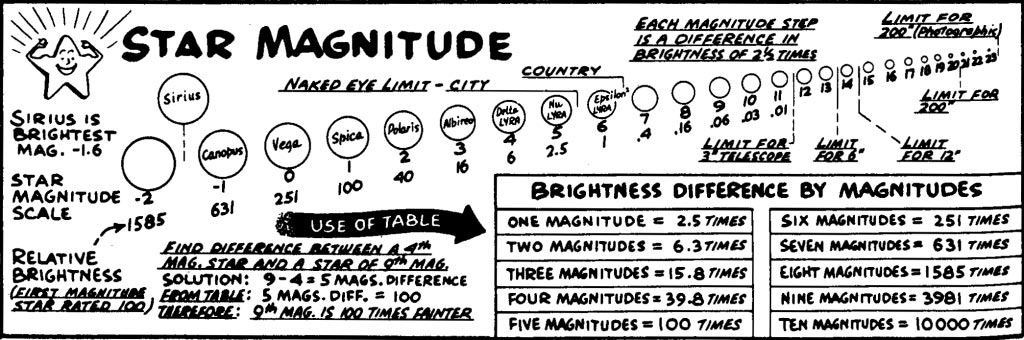 Figure 1 - An infographic that explains the magnitude system with which astronomers measure the brightness of celestial objects. Credit: University of Virginia.
Figure 1 - An infographic that explains the magnitude system with which astronomers measure the brightness of celestial objects. Credit: University of Virginia.The bright star Regulus, which is visible from March through June, is a prominent star of the first magnitude (magnitude 1.36 to be exact). Deneb is a star of magnitude 1.25, while Vega has magnitude +0.03. With your unaided eye, the faintest stars you can see in very dark sky are magnitude 6.5 or so; with a pair of 7×50 binoculars you can see down to magnitude 10.5; and with an 8-inch telescope, perhaps 13.5. Using sophisticated cameras and software, the Hubble Space Telescope can detect objects to about 30th magnitude...about 4 billion times fainter than you can see with your eye.
An object brighter than 0th magnitude has a negative magnitude; the brightest star, Sirius has an apparent magnitude -1.4; the full moon has apparent magnitude -13, and the Sun has apparent magnitude of -26. Don't let negative magnitude confuse you: an object of magnitude -1.0 is simply 2½ times brighter than an object of magnitude 0.0.
Some planets get even brighter than Sirius, the brightest star. Jupiter is always brighter, reaching magnitudes of -2.0 to -2.5 or so. Saturn gets as bright as -0.49. Mars varies from magnitude +2 to -3 approximately. Mercury can reach a magnitude of -2.45. And Venus, when it's closest to Earth and illuminated as a crescent can reach magnitude -4.89, almost bright enough to cast a shadow on dark nights.
Most star charts show the apparent magnitude of stars with their comparative size. Larger circles represent brighter stars (see Figure 2).
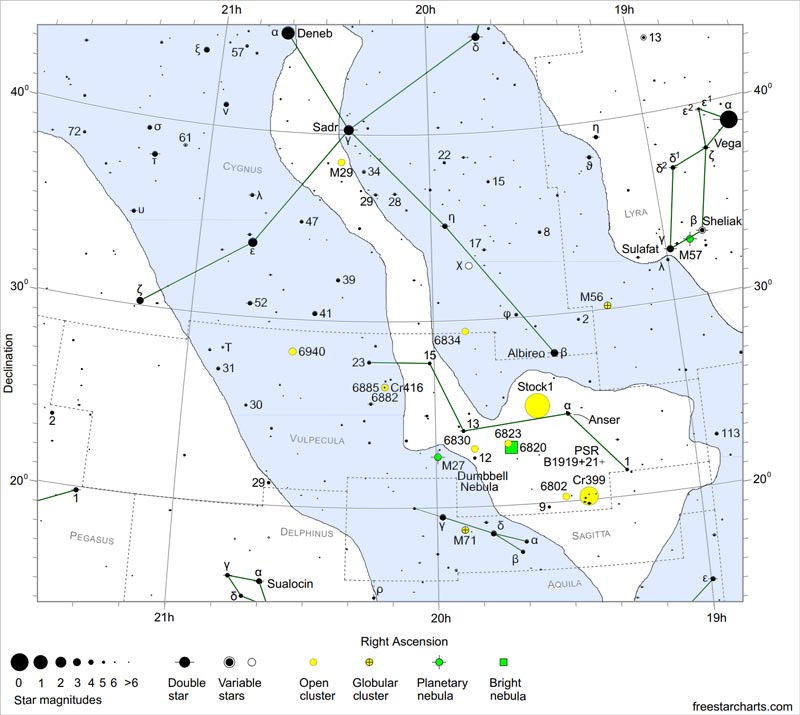 Figure 2 - A star chart showing the comparative magnitudes of the stars. The star Vega has magnitude 0, approximately, while Deneb is a star of the first magnitude. Credit: FreeStarCharts.com.
Figure 2 - A star chart showing the comparative magnitudes of the stars. The star Vega has magnitude 0, approximately, while Deneb is a star of the first magnitude. Credit: FreeStarCharts.com.2. Apparent vs Absolute Magnitude
Usually, backyard stargazers talk about "apparent" magnitude, which measures how bright a star appears in the sky, regardless of how bright it truly is.
"Absolute" magnitude is a measure of the true, intrinsic brightness of a star. It's defined as the apparent magnitude of an object if it were 32.616 light-years away. So while the sun has an apparent magnitude of -26, if we could see it at a distance of 32.616 light-years, it would shine at a very modest magnitude 4.7. Deneb, the brightest star in the constellation Cygnus, has an absolute magnitude of -6.93, nearly 50,000 times brighter than our Sun. But its apparent magnitude is only 1.25 because it's so far away, roughly 1,400 light-years from Earth.
The apparent magnitude, absolute magnitude, and distance to a star are related to each other. If two of these quantities are known, the third can be calculated. For those who are mathematically inclined, here's the relationship:
m - M = 5 (log d - 1)
Here m is the apparent magnitude, M is the absolute magnitude, and d is the distance to the star in parsecs (1 parsec = 3.262 light years). For example, the star Sirius has an apparent magnitude of -1.44. Astronomers can directly measure the distance to the star of 8.60 light years, or 2.64 parsecs. So the absolute magnitude of Sirius is 1.45. Our Sun has an absolute magnitude of 4.7, so Sirius is intrinsically 3.25 magnitudes brighter than the Sun. That's about a factor of 2.512^3.25 = 20 times brighter than our Sun in linear terms.
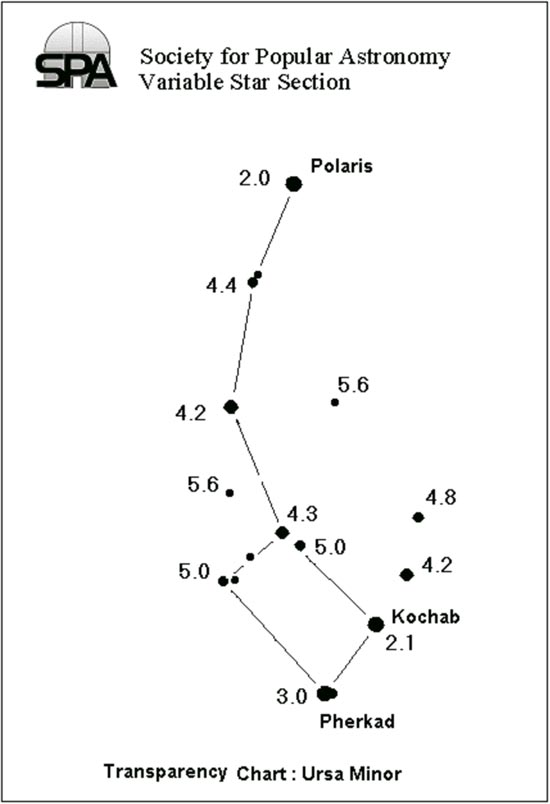 Figure 3 - A chart of the major stars in the Little Dipper range from magnitude 2.0 down to magnitude 5.6. They are useful for evaluating the transparency of the night sky and the effects of light pollution. Credit: Society for Popular Astronomy.
Figure 3 - A chart of the major stars in the Little Dipper range from magnitude 2.0 down to magnitude 5.6. They are useful for evaluating the transparency of the night sky and the effects of light pollution. Credit: Society for Popular Astronomy.3. Evaluating Sky Conditions with Star Magnitudes
Star magnitudes can also be used to evaluate the transparency of the night sky and the effect of light pollution. In clear and dark sky, most people can see stars as faint as magnitude 6.0 to 6.5. In brightly-lit cities, light pollution can limit our ability to see stars fainter than magnitude 3.0 or 4.0. When you hear astronomers talking about 'magnitude 4 sky', for example, they mean stars fainter than magnitude 4.0 are not visible without optical aid because of the effects of light pollution or high cloud and haze.
To estimate the visibility of stars, and to practice your own familiarity with the magnitude system, it's useful to consider the brightest stars of the Little Dipper, an asterism that makes up much of the constellation Ursa Minor. As Figure 3 shows, these stars range from magnitude 2.0 (for Polaris) down to about magnitude 5.6. If you can see all the stars of the Little Dipper as shown in Figure 3, you have good sky. In dry, dark conditions at high altitudes, some stargazers claim to see stars down to magnitude 7!
***
This article is © AstronomyConnect 2017. All rights reserved.
Please login or register to watch, comment, or like this article.
Dismiss Notice
New Cookie Policy
On May 24, 2018, we published revised versions of our Terms and Rules and Cookie Policy. Your use of AstronomyConnect.com’s services is subject to these revised terms.

